Kapitel 8 Visualisierungen
Eine der informativsten und zugänglichsten Form der Darstellung von Unterschieden oder Zusammenhängen ist ein Diagramm. Optisch ansprechende Abbildungen zu erstellen, die dann auch noch für wissenschaftliche Publikationen geeignet sind, war bisher allerdings oftmals ein Krampf. Innerhalb dieses Kapitels wird ein konsistentes Schema zur Erstellung und Anpassung einfacher bis komplexer Abbildungen verschiedener Art vorgestellt und an vielen praktischen Beispielen gefestigt.
8.1 Einführung
Mit R können komplexe und dabei optisch ansprechende Abbildungen erstellt werden, die durch die umfangreichen Anpassungsmöglichkeiten gleichermaßen für wissenschaftlichen Publikationen oder in Unternehmen verwendet werden. Durch das Package ggplot können auf konsistente Art und Weise Histogramme, Streudiagramme, Boxplots, Balkendiagramme, Liniendiagramme und viele mehr erstellt werden. Die zwei g des im tidyverse enthaltenen Packages ggplot stehen für grammar of graphics, was frei als Grammatik der Abbildungen übersetzt werden kann. Für alle Unterkapitel muss folglich das tidyverse installiert und geladen sein.
Überprüfe zunächst, ob die Standardausgabe für deine Abbildungen in den Einstellungen auf AGG gestellt ist (siehe Kapitel 2.3). Weiters werden wir auch hier mit der leicht modifizierten Variante des Big Five Datensatzes arbeiten.
# A tibble: 200 × 6
Alter Geschlecht Extraversion Neurotizismus Gruppe ID
<dbl> <chr> <dbl> <dbl> <fct> <int>
1 36 m 3 1.9 Mittel 1
2 30 f 3.1 3.4 Jung 2
3 23 m 3.4 2.4 Jung 3
4 54 m 3.3 4.2 Weise 4
# ℹ 196 more rowsIn Abbildung 8.1 sind die grundsätzlichen Komponenten einer ggplot Abbildung links und je ein entsprechendes Beispiel rechts abgebildet. Jeder ggplot besteht aus verschiedenen Layern, die untereinander gelegt werden. Um eine Abbildung zu erstellen, muss auf jeden Fall Data, Aestetics und Geometries vorhanden sein. Die Layer namens Scales und Theme sind hingegen optional und passen lediglich das Erscheinungsbild an. Wir werden uns in Kapitel 8.2 bis 8.8 die verschiedenen Geometries Layer anschauen. Erst in Kapitel 8.10 werden die Anpassungsmöglichkeiten mithilfe der Scales und Theme Layer umfangreich erklärt.
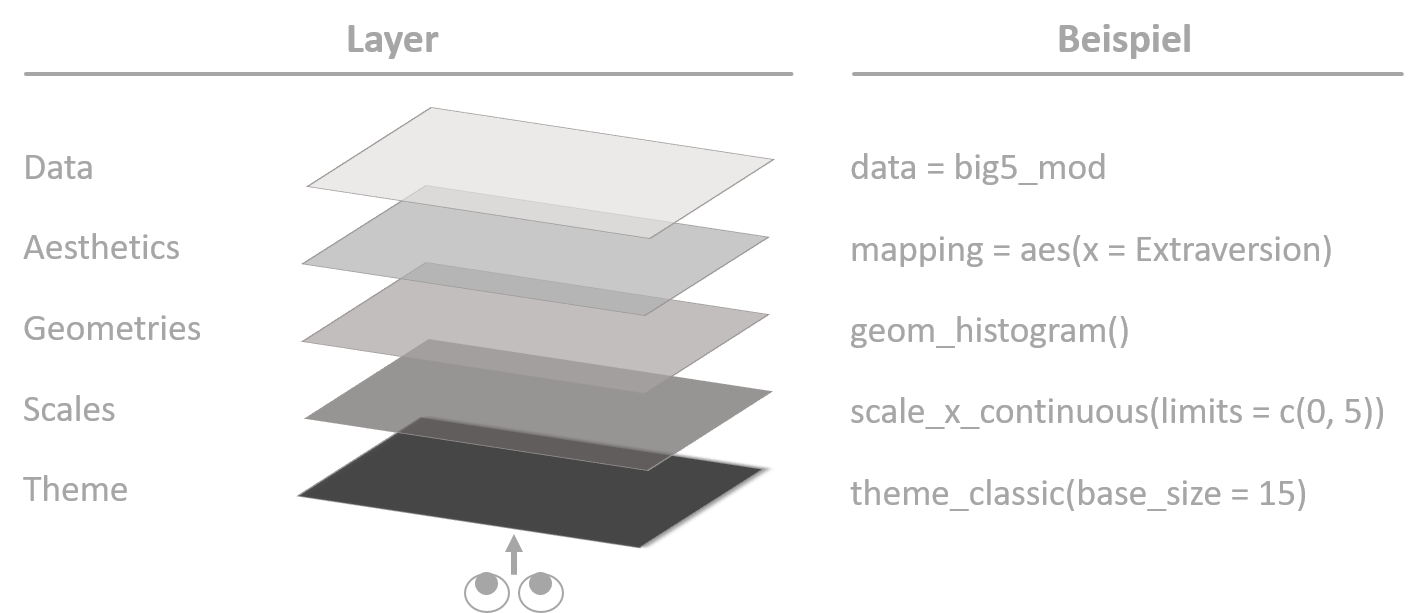
Abbildung 8.1: Vereinfachte Anordnung der Layer im Rahmen der Grammar of Graphics mit Beispielen.
Es ist wichtig zu verstehen, dass die Layer untereinander gelegt werden und man am Ende von unten auf die kreierte Abbildung schaut. Wenn man bspw. mehrere Geometries hintereinander in einen Plot einbaut, kann der zuletzt hinzugefügte den vorherigen vollständig oder teilweise überdecken. Bleiben wir bei dem Beispiel der Erstellung eines Histogramms aus Abbildung 8.1.
Innerhalb der Funktion ggplot() wird dem data Argument der Datensatz big5_mod übergeben. Aus diesem Datensatz möchten wir die Spalte Extraversion auf der x-Achse abbilden. Die ersten beiden Layer sind somit bereits vorhanden. Der Aesthetics Layer wird durch das mapping Argument hinzugefügt. Allerdings können wir die Spalte nicht einfach mit x = Extraversion hinzufügen, sondern benötigen die Helferfunktion aes(), der wir unsere Spalte übergeben. Dabei steht aes() für aesthetics (engl. für Ästhetik).
Neben der Spalte, die auf der x-Achse abgebildet werden soll, kann auf dieselbe Art und Weise die y-Achse definiert werden. Welche Variable dabei auf welcher Achse angezeigt werden soll, kann von dir frei entschieden werden. Auch Argumente zur Veränderung des Aussehens wie color (Außenfarbe) oder fill (Füllfarbe) können hier innerhalb von aes() der Funktion ggplot übergeben werden. Dabei muss für beide Argumente die Spalte Werte vom Typ character oder factor enthalten. Der eigentliche Graph wird erst mit den geom_*() Funktionen hinzugefügt (z.B. geom_histogram()). Das Präfix geom ist dabei für jeden Geometry Layer derselbe.
Wichtig ist an dieser Stelle noch das Pluszeichen (+), welches sämtliche Layer zusammenbindet und untereinander verbindet. Dies unterscheidet sich grundlegend von den restlichen Funktion innerhalb des tidyverse, die mithilfe der Pipe (|>) kombiniert werden (siehe Kapitel 6).
Im Gegensatz zu anderen Funktionen innerhalb des tidyverse können Funktionen aus dem Package ggplot2 nicht mit einer Pipe aneinander gebunden werden. Das hat ausschließlich historische Gründe, da zu der Zeit der Erstellung von ggplot2 die Pipe noch nicht existiert hat. Dies wird sich in Zukunft voraussichtlich auch nicht mehr ändern.
Schauen wir uns die einzelnen Befehle einmal genauer an. Der Data Layer kreiert nur eine leere Fläche (siehe Abbildung 8.2 (a)).
Durch das Hinzufügen des Aesthetics Layers wird ein Raster angefertigt und die x-Achse mit der gewünschten Spalte Extraversion beschriftet (siehe Abbildung 8.2 (b)). Allerdings werden noch immer keine Werte angezeigt, da wir dafür den Geometry Layer benötigen.
Die meisten Funktionen des Geometry Layers beginnen mit dem Präfix geom_ und enden mit dem Namen der Abbildungsart (z.B. geom_histogram() für Histogramme oder geom_boxplot() für Boxplots). Das Ergebnis ist in Abbildung 8.2 (c)) illustriert.
Abbildung 8.2: (a) Nur Data Layer (b) Data und Aesthetics Layer und (c) Data, Aesthetics und Geometry Layer.
Die beiden Namen der Argumente data und mapping schreiben wir im Folgenden nicht mehr explizit aus, weil die Reihenfolge dieser Argumente im Verlaufe des Buches dieselbe ist und es ohne übersichtlicher ist. Da das standardmäßige Aussehen mit dem hellgrauen Hintergrund in dieser Form nicht für wissenschaftliche Publikationen geeignet ist, werden wir in Kapitel 8.10 die notwendigen Anpassungsmöglichkeiten besprechen.
8.2 Histogramm und Dichte
Das Histogramm wurde exemplarisch bereits zur Erklärung des Aufbau eines ggplots in der Einführung beschrieben. Histogramme verwendet man zur Abbildung von Häufigkeitsverteilungen kontinuierlicher Variablen. Zur Erstellung eines Histograms in R bedarf es nur der Zuweisung der interessierenden Variable für die x-Achse, da auf der y-Achse die Häufigkeiten dargestellt werden.
Für ein schlichteres Aussehen fügen wir in Abbildung 8.3 (b) noch eine schwarze Rahmenfarbe mit dem color Argument und eine weiße Füllungsfarbe mit fill hinzu (siehe Kapitel 8.10.1).
Histogramme sind allerdings maßgeblich von der gewählten Breite der Balken abhängig. Bei zu wenigen Balken können Informationen der Verteilung verloren gehen, bei zu vielen hingegen irrelevante Trends erscheinen. Dieses kann entweder direkt mit der Anzahl der Balken (bins Argument) oder mit der Breite (binwidth Argument) verändert werden. Wir werden hier das Argument binwidth verwenden, da diesem auch eine Funktion übergeben werden kann.
ggplot(big5_mod, aes(x = Extraversion)) +
geom_histogram(
color = "black",
fill = "white",
binwidth = 0.2
)
Abbildung 8.3: Histogramme im Vergleich.
Es gibt verschiedene Arten, eine möglichst optimale binwidth herauszufinden. Exemplarisch sei hier die Freedman-Diaconis Regel angewandt. Diese können wir mithilfe einer neuen anonymen Funktion dem binwidth Argument übergeben (siehe Kapitel 6.4.4). Das Ergebnis ist in Abbildung 8.4 (a) gezeigt.
ggplot(big5_mod, aes(x = Extraversion)) +
geom_histogram(
color = "black",
fill = "white",
binwidth = \(x) (max(x) - min(x)) / nclass.FD(x)
)Eine weitere Möglichkeit, die Verteilung der Extraversion unserer Population darzustellen, ist die Wahrscheinlichkeitsdichte. Dazu müssen wir lediglich das Suffix des Geometry Layers zu density (engl. für Dichte) verändern (siehe Abbildung 8.4 (b)).
Um das Histogramm gemeinsam mit der Wahrscheinlichkeitsdichte abzubilden, müssen sich beide auf derselben Skala befinden. Zum Beispiel könnte man die Häufigkeiten des Histogramms ebenfalls als Dichte ausdrücken. Dafür muss dem height und y Argument jeweils die berechnete Dichte (density) übergeben werden. Diese wird mithilfe der Helferfunktion after_stat() berechnet.
Anschließend muss lediglich mit einem weiteren Pluszeichen die Dichtefunktion hinzugefügt werden. Für eine ansprechendere optische Darstellung sei eine graue Füllfarbe ergänzt, welche mithilfe des alpha Argument etwas durchsichtig wird. Das Ergebnis kann in Abbildung 8.4 (c) betrachtet werden.
ggplot(big5_mod, aes(x = Extraversion, height = after_stat(density))) +
geom_histogram(
mapping = aes(y = after_stat(density)),
binwidth = 0.2,
color = "black",
fill = "white"
) +
geom_density(fill = "grey", alpha = 0.7)
Abbildung 8.4: Histogramm und Wahrscheinlichkeitsdichte separat und kombiniert.
8.3 Streudiagramm
Das Erstellen eines Streudiagramms in R benötigt das Festlegen der x-Achse und y-Achse (auch Punktdiagramm oder Scatter Plot genannt). Im Vergleich zum bereits kennengelernten Histogramm ändert sich sonst nur der Geometry Layer zu geom_point(). Exemplarisch sei hier die mittlere Extraversion gegen das Lebensalter in Jahren aufgetragen (siehe Abbildung 8.5 (a)). Auf weitere Parameter wie das Ändern der Farbe (color) oder Form (shape) verzichten wir an dieser Stelle.
Bei größeren Datensätzen oder generell bei kategorealen Variablen kann es passieren, dass die Punkte sich überlappen. Um das zu verhindern, kann die Position zu jitter verändert werden. Dies bewirkt eine leichte zufällige Variation jedes Datenpunktes, welche vor allem für die explorative Betrachtung in Frage kommt und nur zurückhaltend für Publikationen vorgesehen ist, da die Erhebungsskala so verschleiert wird (siehe Abbildung 8.5 (b)).
Mit geom_smooth() wird eine am besten passende Linie durch die Punkte gezogen. Wir entscheiden uns an dieser Stelle für eine lineare Regressionsgeraden (method = lm). Außerdem färben wir die Gerade schwarz und fügen ein 95%iges Konfidenzintervall mit se = TRUE hinzu.
Damit die Regressionsgerade nicht nur in dem Bereich, in dem Daten beobachtet wurden, abgebildet wird, kann zusätzlich das fullrange Argument auf TRUE gesetzt werden. Um den Effekt dieser Funktion zu illustrieren, greifen wir etwas voraus und definieren mit xlim(c(2, 5)) die untere Grenze der x-Achse mit 2 und die obere mit 5 (siehe Abbildung 8.5 (c)).
ggplot(big5_mod, aes(x = Extraversion, y = Alter)) +
geom_point(position = "jitter") +
geom_smooth(
color = "black",
method = lm,
se = TRUE,
fullrange = TRUE
) +
xlim(c(2, 5)) 
Abbildung 8.5: Streudiagramm mit und ohne Regressionsgerade.
8.4 Boxplot
Würde man nur einen Boxplot für die mittlere Ausprägung von Extraversion erstellen wollen, könnte man dies genau wie in den beiden zuvor besprochenen Kapiteln durch das Auswechseln des Geometry Layers mit geom_boxplot() erreichen (siehe Abbildung 8.6 (a)).
Dies stellt allerdings eine seltene Situation dar. Meistens ist man am Vergleich mehrerer Variablen interessiert, die auf der x-Achse aufgetragen werden.
An dieser Stelle sollen die Verteilungen von Extraversion und Neurotizismus miteinander verglichen werden. Um dies zu erreichen, müssen wir den Datensatz vom breiten ins lange Datenformat transformieren (siehe Kapitel 6.6). Dafür wird die Funktion pivot_longer() verwendet.
big5_long <- big5_mod |>
pivot_longer(
cols = Extraversion:Neurotizismus,
names_to = "Faktor",
values_to = "Auspraegung"
)# A tibble: 400 × 7
Alter Geschlecht Gruppe ID Faktor Auspraegung Zeitpunkt
<dbl> <chr> <chr> <int> <chr> <dbl> <chr>
1 36 m Mittel 1 Extraversion 3 T1
2 36 m Mittel 1 Neurotizismus 1.9 T1
3 30 f Jung 2 Extraversion 3.1 T1
4 30 f Jung 2 Neurotizismus 3.4 T1
# ℹ 396 more rowsNach der Umwandlung sind in big5_long die Persönlichkeitsfaktoren in der Spalte Faktor und die Extraversions- und Neurotizismusausprägung in der Spalte Auspraegung.
Einen Boxplot erstellt man mit geom_boxplot(). Auf der x-Achse möchten wir die Persönlichkeitsfaktoren und auf der y-Achse die mittleren Ausprägungen darstellen (siehe Abbildung 8.6 (b)).
Um zusätzlich Fehlerbalken zu erhalten, müssen diese mit stat_boxplot() berechnet werden. Das Argument geom muss auf "errorbar" (engl. für Fehlerbalken) gesetzt werden. Die Breite des Fehlerbalkens kann durch das optionale Argument width kontrolliert werden. Zum Ausblenden der Ausreißer setzt man innerhalb von geom_boxplot() das Argument outlier.shape auf NA (Akronym für Not Available, engl. für nicht vorhanden). Alternativ können die Ausreißer mit outliers = FALSE entfernt werden. Der Unterschied besteht darin, dass bei letzterem Fall zusätzlich die Grenzen der Achsen verändert werden. Ausreißer sollten nur nach sorgfältigem Hinterfragen ausgeblendet werden, schließlich sind bei weitem nicht alle Ausreißer auf Datenfehler zurückzuführen. Das Ergebnis ist in Abbildung 8.6 (c) illustriert.
ggplot(big5_long, aes(x = Faktor, y = Auspraegung)) +
stat_boxplot(geom = "errorbar", width = 0.4) +
geom_boxplot(outlier.shape = NA) 
Abbildung 8.6: Boxplots im Vergleich.
Beim Hinzufügen von Fehlerbalken ist die Reihenfolge der Funktionsaufrufe entscheidend, da die verschiedenen Layer untereinander gezeichnet werden. Würden wir also zunächst geom_boxplot() und erst anschließend stat_boxplot() zum ggplot hinzufügen, würde die Linie des Fehlerbalkens über dem Boxplot abgebildet werden.
8.5 Violin Plot
Im Vergleich zu Boxplots ändert sich zum einen der Geometry Layer, welcher nun geom_violin() heißt und zum anderen muss noch eine willkürliche Koordinate für die x-Achse gewählt werden (hier 0) (siehe Abbildung 8.7 (a)). Zusätzlich zu den Informationen des Boxplots wird hier die Wahrscheinlichkeitsdichte abgebildet. Je breiter die Abbildung an einer bestimmten Stelle ist, desto mehr Datenpunkte finden sich dort.
Für mehrere Violin Plots nutzen wir genau wie zuvor bei den Boxplots den Datensatz im langen Datenformat namens big5_long (siehe Kapitel 8.4 und 6.6). Auch hier werden auf der x-Achse die Persönlichkeitsfaktoren und auf der y-Achse die jeweilige Ausprägung ausgegeben (siehe Abbildung 8.7 (b)).
Optional kann zusätzlich das Argument trim auf FALSE gesetzt werden, um das Abschneiden der Enden des Violin Plots zu verhindern. Mithilfe des Arguments draw_quantiles können wir explizit beliebige Quantile (hier Quartile) einzeichnen lassen. Das Ergebnis ist in Abbildung 8.7 (c) zu sehen.
ggplot(big5_long, aes(x = Faktor, y = Auspraegung)) +
geom_violin(
trim = FALSE,
draw_quantiles = c(0.25, 0.5, 0.75)
)
Abbildung 8.7: Violin Plots im Vergleich.
8.6 Balkendiagramm
In einem Balkendiagramm werden im Regelfall entweder Häufigkeiten oder Mittelwerte miteinander verglichen (auch Säulendiagramm oder Barplot genannt). Zum Darstellen absoluter Häufigkeiten kategorealer Variablen wird die Funktion geom_bar() verwendet. Wir können dabei frei entscheiden, ob die Balken vertikal oder horizontal angeordnet werden sollen. Für eine vertikale Illustration auf der x-Achse übergeben wir die Spalte Geschlecht dem x Argument (siehe Abbildung 8.8) (a)).
Äquivalent dazu können wir horizontale Balkendiagramme durch Abbildung der entsprechenden Spalte auf der y-Achse mit dem y Argument erstellen (siehe Abbildung 8.8) (b)).
Anstelle von absoluten Häufigkeiten können ebenfalls relative Häufigkeiten verglichen werden. Hierzu müssen wir innerhalb der Helferfunktion after_stat() das Argument prop übergeben und zeitgleich das group Argument auf 1 setzen (siehe Abbildung 8.8) (c)). Diese Helferfunktion haben wir bereits im Kontext der Histogramme in Kapitel 8.2 kennengelernt.
Möchten wir Mittelwerte miteinander vergleichen, müssen wir auf die Funktion geom_col() zurückgreifen. Beim Gegenüberstellen mehrerer Merkmale, wird zunächst, wie bereits in den Kapiteln 8.4 und 8.5 bei den Boxplots und Violin Plots kennengelernt, der Datensatz in ein langes Format gebracht (siehe Kapitel 6.6).
big5_long <- big5_mod |>
pivot_longer(
cols = Extraversion:Neurotizismus,
names_to = "Faktor",
values_to = "Auspraegung"
)# A tibble: 400 × 7
Alter Geschlecht Gruppe ID Faktor Auspraegung Zeitpunkt
<dbl> <chr> <chr> <int> <chr> <dbl> <chr>
1 36 m Mittel 1 Extraversion 3 T1
2 36 m Mittel 1 Neurotizismus 1.9 T1
3 30 f Jung 2 Extraversion 3.1 T1
4 30 f Jung 2 Neurotizismus 3.4 T1
# ℹ 396 more rowsDie abzubildenden Mittelwerte und Standardabweichungen berechnen wir vor der Visualisierung und speichern das Zwischenergebnis als big5_means ab. Die Standardabweichungen benötigen wir für die Fehlerbalken. Alternativ könnte man durch Teilen der Standardabweichung durch die Stichprobengröße auch den Standardfehler abbilden. Wie man diese Lage- und Streuungsmaße berechnet, wurde bereits in Kapitel 7.1 eingeführt.
big5_means <- big5_long |>
group_by(Faktor) |>
summarise(
Mean = mean(Auspraegung, na.rm = TRUE),
SD = sd(Auspraegung, na.rm = TRUE)
)
big5_means# A tibble: 2 × 3
Faktor Mean SD
<chr> <dbl> <dbl>
1 Extraversion 3.08 0.347
2 Neurotizismus 3.13 0.682Die Balken werden mit geom_col() erstellt. Auf der x-Achse sind demnach wie zuvor auch die Persönlichkeitsfaktoren und auf der y-Achse die Mittelwerte aufgetragen (siehe Abbildung 8.8 (d)).
Verwechsle geom_col() nicht mit geom_bar(). Erstere Funktion stellt genau das dar, was man ihr übergibt (z.B. Mittelwerte). Letztere Funktion hingegen erstellt Balken mit absoluten oder relativen Häufigkeiten.
Um das Balkendiagramm zu verschönern, können wir auch hier die Füllfarbe (fill) und die Rahmenfarbe (color) entsprechend anpassen (siehe Abbildung 8.8 (e)).
Zusätzlich bilden wir mit der Funktion geom_errorbar() die Standardabweichung (SD) ab, indem das Minimum des Fehlerbalken als Mittelwert minus der Standardabweichung und das Maximum als Mittelwert plus der Standardabweichung festlegt wird. Die Breite der Fehlerbalken wird mit dem Argument width verändert. Beachte an dieser Stelle, dass die Grenzen der Fehlerbalken (ymin und ymax) im Gegensatz zur Fehlerbalkenbreite innerhalb der Helferfunktion aes() definiert werden müssen. Das Ergebnis ist in Abbildung 8.8 (f) illustriert.
ggplot(big5_means, aes(x = Faktor, y = Mean)) +
geom_col(fill = "white", color = "black") +
geom_errorbar(
mapping = aes(ymin = Mean - SD, ymax = Mean + SD),
width = 0.4
)Falls du mehr als eine Gruppe innerhalb eines Balkendiagramms vergleichen möchtest, musst du ein Gruppierungsargument verwenden, welches in Kapitel 8.9 eingeführt wird.
Abbildung 8.8: Verschiedene Balkendiagramme mit und ohne Fehlerbalken.
8.7 Liniendiagramm
Bei Mittelwertvergleichen in Form von Liniendiagrammen ändert sich im Vergleich zu den Balkendiagrammen nur wenig. Auch hier verwenden wir wieder den Datensatz big5_means, der unsere Mittelwerte und Standardabweichungen für Extraversion und Neurotizismus enthält (siehe Kapitel 8.6.
Zum Erstellen der Verbindungslinie zwischen den beiden Persönlichkeitsfaktoren muss das group Argument auf 1 gesetzt werden. Abschließend müssen wir noch die Linie mit geom_line(), die Mittelwerte als Punkte mit geom_point() und die Fehlerbalken mit geom_errorbar() erstellen. Auch bei den Fehlerbalken ändert sich nichts im Vergleich zu den Balkendiagrammen. Das Ergebnis ist in Abbildung 8.9 (a) illustriert.
ggplot(big5_means, aes(x = Faktor, y = Mean, group = 1)) +
geom_line() +
geom_point() +
geom_errorbar(
mapping = aes(ymin = Mean - SD, ymax = Mean + SD),
width = 0.2
) Ein weiteres klassisches Beispiel eines Liniendiagramms ist die Abbildung von Zeitreihen. Dafür schauen wir uns den Kurs der Bitcoin-Aktie an.
# A tibble: 731 × 2
Datum Preis
<date> <dbl>
1 2019-01-01 3844.
2 2019-01-02 3943.
3 2019-01-03 3837.
4 2019-01-04 3858.
# ℹ 727 more rowsAuf der x-Achse soll das Datum und auf der y-Achse der Preis bei geschlossener Börse in USD abgebildet werden. Die Zeitreihe wird wie zuvor mit geom_line() visualisiert. Wichtig ist hierbei, dass das Datum vom Datentyp Date ist (siehe Kapitel 6.11). Zusätzlich können wir, wie beim Streudiagramm in Kapitel 8.3, mit stat_smooth() eine am besten passendste Kurve zur Kursbeschreibung hinzufügen.
Abschließend greifen wir an dieser Stelle etwas vor und verändern noch die Benennung der x-Achse mithilfe von scale_x_date(). Dabei gibt es verschiedene Möglichkeiten der Anzeige, die jeweils mit einem Prozentzeichen angeführt werden müssen. Hier zeigen wir den abgekürzten Monatsnamen (%b) und das entsprechende Jahr (%Y). Das Ergebnis ist in Abbildung 8.9 (b) illustriert.
ggplot(bitcoin, aes(x = Datum, y = Preis)) +
geom_line() +
stat_smooth(color = "black") +
scale_x_date(date_labels = "%b %Y")Eine weitere Anwendung finden Liniendiagramme bei sogenannten Scree Plots zur Auswahl der Anzahl der Faktoren für explorative Faktorenanalysen. Dafür benötigen wir den kompletten Big 5 Datensatz mit den einzelnen Fragen zu den Persönlichkeitsfaktoren namens big5_comp. Mit der im remp Package enthaltenen Funktion data_eigen() können die entsprechenden Eigenvalues berechnet werden, die wir im Scree Plot abbilden wollen.
# A tibble: 51 × 2
Eigenwerte Dimension
<dbl> <int>
1 8.25 1
2 4.59 2
3 3.62 3
4 3.57 4
# ℹ 47 more rowsAuf der x-Achse haben wir unsere verschiedenen Dimensionen und auf der y-Achse die Eigenwerte. Zusätzlich modifizieren wir die Funktionen geom_point() und geom_line() optisch leicht. Neu ist an dieser Stelle die Funktion geom_hline() (für horizontal line), welche eine horizontale Linie beim Schnittpunkt mit der y-Achse von 1 einzeichnet (siehe Abbildung 8.9 (c)).
ggplot(big5_scree, aes(x = Dimension, y = Eigenwerte)) +
geom_point(shape = 19, size = 2) +
geom_line(linewidth = 0.6) +
geom_hline(
mapping = aes(yintercept = 1),
linewidth = 0.8,
linetype = "longdash"
) 
Abbildung 8.9: Abbildung von Liniendiagrammen als (a) Mittelwertsvergleich (b) Zeitreihe und (c) Scree Plot
8.8 Quantil-Quantil Plot
Um mithilfe eines Q-Q Plots die Quantile zweier Verteilungen zu überprüfen, verwenden wir die Funktionen geom_qq() und geom_qq_line(). Ein häufiger Anwendungsfall ist die graphische Überprüfung auf Vorliegen einer Normverteilung eines intervallskalierten Merkmals oder der Residuen eines Regressionsmoodells. Daher ist der Vergleich mit einer Normalverteilung auch die Standardeinstellung innerhalb der Funktionen.
Die interessierende Variable könnte bspw. die Leukozytenanzahl nach 6 Monaten Therapie sein (Leukos_t6), welche im chemo Datensatz enthalten ist. Diese übergeben wir dem sample Argument (engl. für Stichprobe) (siehe Abbildung 8.10).
Abbildung 8.10: Q-Q Plots
Möchte man die Verteilung eines Merkmals mit einer anderen Verteilung vergleichen, könnten wir mit dem distribution Argument die Quantile einer anderen Verteilung wie der Binomialverteilung (qbinom) oder der t-Verteilung (qt) festlegen. Beachte, dass hierbei keine Anführungszeichen verwendet werden. Bei der Überprüfung von Residuen werden dem sample Argument stattdessen die geschätzten Residuen übergeben (siehe Kapitel 8.13.2, 9.7.1 und 9.8).
8.9 Mehrfaktorielle Abbildungen
In den bisherigen Abbildungen haben wir bislang nur jeweils zwei Variablen in Zusammenhang gesetzt, indem eine Variable auf der x-Achse und eine auf der y-Achse visualisiert wurde. Eine dritte Variable kann mit dem Gruppierungselement hinzugefügt werden (siehe Kapitel 8.9.1). Für das zeitgleiche Vergleichen einer vierten und fünften Variable innerhalb einer Abbildungen können sogenannte Facetten erstellt werden (siehe Kapitel 8.9.2).
8.9.1 Gruppierungsargumente
Gruppierungen können in Abhängigkeit der gewünschten Darstellung durch die Argumente color, fill, linetype, size oder shape innerhalb der Helferfunktion aes() erstellt werden. Anders als bisher wird diesen Argumenten in diesem Fall kein Character (z.B. color = "black"), sondern das gruppierende Argument ohne Anführungszeichen übergeben (z.B. color = Geschlecht).
Als Gruppierungsargumente können nur Spalten vom Datentyp character oder factor gewählt werden. Zum Beispiel könnte eine Spalte namens Geschlecht mit 1 für Männer und 2 für Frauen kodiert sein. Um eine Aufteilung nach Geschlecht umzusetzen, könnten wir direkt im ggplot Aufruf die Spalte Geschlecht nur für die Erstellung der Abbildung in einen Faktor umwandeln (color = factor(Geschlecht)).
Für einige Abbildungen wie bei Mittelwertsvergleichen in Form von Balken- oder Liniendiagrammen benötigen wir ein zusätzliches position Argument. Dieses spezifiziert, wie die Gruppen zueinander in Verhältnis zu setzen sind. Eine nützliche Wahl ist hierfür die Funktion position_dodge(0.95) (engl. für ausweichen), welche die Gruppen direkt nebeneinander darstellt. Die Zahl in der Klammer steht für den genauen Abstand zwischen den Elementen.
Alternativ könnte man bei Balkendiagrammen auch position = "stack" für eine aufeinander gestapelte Ansicht pro Kategorie verwenden. Wenn man stattdessen position = "fill" verwendet, werden diese übereinander gestapelten Anteile auf 1 standardisiert, sodass man die Verhältnisse besser vergleichen kann.
Zum Abbilden der mittleren Ausprägung von Extraversion und Neurotizismus unterteilt nach Geschlecht in Form eines Boxplots verwenden wir den Datensatz big5_long aus dem remp Package.
# A tibble: 400 × 7
Alter Geschlecht Gruppe ID Faktor Auspraegung Zeitpunkt
<dbl> <chr> <chr> <int> <chr> <dbl> <chr>
1 36 m Mittel 1 Extraversion 3 T1
2 36 m Mittel 1 Neurotizismus 1.9 T1
3 30 f Jung 2 Extraversion 3.1 T1
4 30 f Jung 2 Neurotizismus 3.4 T1
# ℹ 396 more rowsDie Füllfarbe (fill) machen wir abhängig vom Geschlecht und das Positionsargument wird ebenfalls entsprechend angepasst werden. Das Ergebnis ist in Abbildung 8.11 (a) illustriert.
ggplot(big5_long, aes(x = Faktor, y = Auspraegung, fill = Geschlecht)) +
geom_boxplot(outlier.shape = NA, position = position_dodge(0.95)) Falls zusätzlich ein Fehlerbalken angezeigt werden soll, muss auch in stat_boxplot() das Positionsargument verwendet werden (siehe Abbildung 8.11 (b)).
ggplot(big5_long, aes(x = Faktor, y = Auspraegung, fill = Geschlecht)) +
stat_boxplot(
geom = "errorbar",
width = 0.4,
position = position_dodge(0.95)
) +
geom_boxplot(outlier.shape = NA, position = position_dodge(0.95)) 
Abbildung 8.11: Boxplots mit und ohne Fehlerbalken nach drei Variablen gruppiert.
Wenn Mittelwerte in Form von Balken- oder Liniendiagrammen unterteilt nach einer dritten Variable miteinander verglichen werden sollen, müssen diese zuerst berechnet werden (siehe Kapitel 7). Dabei müssen wir zusätzlich nach der dritten Variable (hier Geschlecht) gruppieren.
big5_means2 <- big5_long |>
group_by(Faktor, Geschlecht) |>
summarise(
Mean = mean(Auspraegung, na.rm = TRUE),
SD = sd(Auspraegung, na.rm = TRUE)
)
big5_means2# A tibble: 4 × 4
# Groups: Faktor [2]
Faktor Geschlecht Mean SD
<chr> <chr> <dbl> <dbl>
1 Extraversion f 3.05 0.358
2 Extraversion m 3.11 0.328
3 Neurotizismus f 3.25 0.633
4 Neurotizismus m 2.96 0.718Ansonsten ändert sich im Vergleich zum vorherigen Beispiel nichts. Auch hier muss die Füllfarbe (fill = Geschlecht) und die Position der gruppierten Balken definiert werden. Das Ergebnis ist in Abbildung 8.12 (a) illustriert.
ggplot(big5_means2, aes(x = Faktor, y = Mean, fill = Geschlecht)) +
geom_col(position = position_dodge(0.95), color = "black") +
geom_errorbar(
mapping = aes(ymin = Mean - SD, ymax = Mean + SD),
width = 0.4,
position = position_dodge(0.95)
) Ein weiterer Anwendungsfall sind gruppierte Liniendiagramme. Hierfür ändern wir an dieser Stelle das Argument fill zu linetype. Zusätzlich muss das Gruppierungsargument (hier Geschlecht) den einzelnen Funktionen übergeben werden, da sonst keine Linien zwischen den Gruppen gezeichnet werden würden (siehe Abbildung 8.12 (b)).
ggplot(big5_means2, aes(x = Faktor, y = Mean, linetype = Geschlecht)) +
geom_line(
mapping = aes(group = Geschlecht),
position = position_dodge(0.2)
) +
geom_point(position = position_dodge(0.2)) +
geom_errorbar(
mapping = aes(group = Geschlecht, ymin = Mean - SD, ymax = Mean + SD),
width = 0.2,
position = position_dodge(0.2)
) 
Abbildung 8.12: Balken- und Liniendiagramme mit drei Variablen.
8.9.2 Facetten als weitere Dimensionen
Für das Hinzufügen einer vierten Variable ändert sich im Vergleich zu Kapitel 8.9.1 nur die zusätzliche Funktion facet_wrap(), welche die vierte Variable in Form einer sogenannten Facette abbildet. Auch hier verwenden wir den big5_long Datensatz aus dem remp Package.
# A tibble: 400 × 7
Alter Geschlecht Gruppe ID Faktor Auspraegung Zeitpunkt
<dbl> <chr> <chr> <int> <chr> <dbl> <chr>
1 36 m Mittel 1 Extraversion 3 T1
2 36 m Mittel 1 Neurotizismus 1.9 T1
3 30 f Jung 2 Extraversion 3.1 T1
4 30 f Jung 2 Neurotizismus 3.4 T1
# ℹ 396 more rowsInnerhalb von facet_wrap() wird erst eine Tilde und anschließend der gewünschte Spaltenname geschrieben. Zusätzliche könnte man mit dem Argument ncol die Anzahl der Spalten festlegen.
ggplot(big5_long, aes(x = Faktor, y = Auspraegung, fill = Geschlecht)) +
geom_boxplot(outlier.shape = NA, position = position_dodge(0.95)) +
facet_wrap(~ Gruppe)
Abbildung 8.13: Boxplot mit vier Variablen.
Wir sehen in Abbildung 8.13, dass die Altersgruppen in einem Raster als separate Graphen angezeigt werden. Die Anzahl der Spalten in der Anordnung können mit dem ncol Argument angepasst werden (z.B. ncol = 2). Mit dem scales Argument ist es möglich, die x-Achse (scales = "free_x") oder y-Achse (scales = "free_y") auf unterschiedlichen Skalen anzeigen zu lassen.
Äquivalent zum Abbilden von drei Variablen in Kapitel 8.9.1, müssen beim Mittelwertsvergleich in Form von Balken- oder Liniendiagrammen auch hier erst die entsprechenden Werte berechnet werden. Der Unterschied ist die zusätzlich gruppierende Variable (hier Gruppe) innerhalb von group_by() (siehe Kapitel 7).
big5_means3 <- big5_long |>
group_by(Faktor, Geschlecht, Gruppe) |>
summarise(
Mean = mean(Auspraegung, na.rm = TRUE),
SD = sd(Auspraegung, na.rm = TRUE)
)
big5_means3# A tibble: 12 × 5
# Groups: Faktor, Geschlecht [4]
Faktor Geschlecht Gruppe Mean SD
<chr> <chr> <chr> <dbl> <dbl>
1 Extraversion f Jung 3.07 0.373
2 Extraversion f Mittel 3.07 0.299
3 Extraversion f Weise 2.83 0.269
4 Extraversion m Jung 3.12 0.324
# ℹ 8 more rowsAnschließend können auf dieselbe Art und Weise mithilfe von facet_wrap() die Altersgruppen eingefügt werden.
ggplot(big5_means3, aes(x = Faktor, y = Mean, fill = Geschlecht)) +
geom_col(position = position_dodge(0.95), color = "black") +
geom_errorbar(
mapping = aes(ymin = Mean - SD, ymax = Mean + SD),
width = 0.4,
position = position_dodge(0.95)
) +
facet_wrap(~ Gruppe) Auch beim Hinzufügen einer fünften Variable finden wir das gleiche Prinzip vor. Für fünf Variablen ändert sich die Funktion zu facet_grid(). Die Variable, welche in den Zeilen des Rasters (hier Zeitpunkt) abgebildet werden soll, wird auf die linke Seite der Tilde und die Variable für die Spalten (hier Gruppe) auf die rechte Seite geschrieben.
ggplot(big5_long, aes(x = Faktor, y = Auspraegung, fill = Geschlecht)) +
geom_boxplot(outlier.shape = NA, position = position_dodge(0.95)) +
facet_grid(Zeitpunkt ~ Gruppe)
Abbildung 8.14: Boxplot mit fünf Variablen.
Bei Mittelwertsvergleichen müssen diese mit group_by() und summarise() durch das Hinzufügen einer vierten gruppierenden Variable zunächst berechnet werden.
big5_means4 <- big5_long |>
group_by(Faktor, Geschlecht, Gruppe, Zeitpunkt) |>
summarise(
Mean = mean(Auspraegung, na.rm = TRUE),
SD = sd(Auspraegung, na.rm = TRUE)
)
big5_means4# A tibble: 24 × 6
# Groups: Faktor, Geschlecht, Gruppe [12]
Faktor Geschlecht Gruppe Zeitpunkt Mean SD
<chr> <chr> <chr> <chr> <dbl> <dbl>
1 Extraversion f Jung T1 3.08 0.391
2 Extraversion f Jung T2 3.06 0.362
3 Extraversion f Mittel T1 2.93 0.121
4 Extraversion f Mittel T2 3.13 0.336
# ℹ 20 more rowsAnschließend kann auch hier ein Raster mithilfe von facet_grid() erstellt werden.
8.10 Anpassen des Aussehens
Die Standardeinstellungen von ggplot sind praktisch für einen ersten Überblick, aber eignen sich nicht zur Veröffentlichung der Abbildungen in einer wissenschaftlichen Publikation. In den folgenden Kapiteln wird erklärt, wie man Farben, Texte, die Legende, die Achsen und vieles mehr verändert.
Wir werden uns anhand der Abbildung aus Kapitel 8.9.1 die verschiedenen Anpassungsmöglichkeiten anschauen. Dabei verwenden wir ebenfalls den Datensatz big5_long im langen Format aus aus dem remp Package.
# A tibble: 400 × 7
Alter Geschlecht Gruppe ID Faktor Auspraegung Zeitpunkt
<dbl> <chr> <chr> <int> <chr> <dbl> <chr>
1 36 m Mittel 1 Extraversion 3 T1
2 36 m Mittel 1 Neurotizismus 1.9 T1
3 30 f Jung 2 Extraversion 3.1 T1
4 30 f Jung 2 Neurotizismus 3.4 T1
# ℹ 396 more rowsZusätzlich fügen wir bereits an dieser Stelle das alpha Argument hinzu, welches die Deckkraft mit 0.8 auf 80% herabsetzt. Dies sorgt für ein subjektiv hochwertigeres Aussehen der Farben. Der gruppierte Boxplot wird als p gespeichert und in den folgenden Kapiteln wiederverwendet.
p <- ggplot(big5_long, aes(x = Faktor, y = Auspraegung, fill = Geschlecht)) +
geom_boxplot(outlier.shape = NA, position = position_dodge(0.95), alpha = 0.8)In Abbildung 8.15 ist die Standardeinstellung von ggplot unserer modifizierten Abbildungen gegenübergestellt. Die verschiedenen Anpassungen können ebenfalls mit einem Pluszeichen (+) aneinandergekettet werden. Wofür welche Funktion genau zuständig ist, wird im weiteren Verlauf kleinschrittig eingeführt.
p +
scale_fill_brewer(
palette = "Dark2",
name = "Geschlecht (Auswahl):",
labels = c("Weiblich", "Männlich")
) +
scale_y_continuous(expand = c(0, 0), limits = c(1, 5.2), breaks = 1:5) +
labs(x = "Persönlichkeitsfaktor", y = "Mittlere Ausprägung") +
theme_classic(base_size = 14, base_family = "sans") +
theme(
legend.position.inside = c(0.4, 0.9),
axis.title.y = element_text(vjust = 2),
axis.title.x = element_text(vjust = 0.5),
axis.text = element_text(size = 13)
) 
Abbildung 8.15: Standardausgabe im Vergleich mit einer publikationsreifen Abbildung.
8.10.1 Farben
Beim Verändern der Farben innerhalb einer Abbildung unterscheiden wir zwischen der Rahmenfarbe (color) und Füllfarbe (fill). Während die Rahmenfarbe häufig als schwarz gewählt werden sollte, hat man mit der Füllfarbe mehr Freiheiten.
Das Farbschema kann durch verschiedene Farbpaletten adaptiert werden. Häufig sind im wissenschaftlichen Kontext jedoch nur Graustufen erwünscht, welche wir mit scale_fill_grey() erstellen können. Wichtig ist an dieser Stelle das start und end Argument der Farbpalette, da die Grautöne sonst zu dunkel für das Erkennen von Fehlerbalken sein können. Hätten wir in unserem ggplot nicht die Füllfarbe (fill), sondern die Rahmenfarbe (color) verändert, würde man stattdessen die Funktion scale_color_grey() verwenden.
Die brewer Paletten enthalten verschiedene Farben wie blau ("Blues") oder rot ("Reds"). Diese werden mit der Funktion scale_fill_brewer() erstellt. Mithilfe von scale_fill_manual() können Farben in Form von Hexadezimal Farbkodierungen als einzelne Werte übergeben werden.
a <- p + scale_fill_grey(start = 0.3, end = 0.7)
b <- p + scale_fill_brewer(palette = "Blues")
c <- p + scale_fill_manual(values = c("#A50F15", "#FC9272"))
Abbildung 8.16: Vergleich verschiedener Farbpaletten.
Bei der Auswahl einzelner Werte sollte ebenfalls auf Farben innerhalb von Paletten zurückgegriffen werden, da diese aufeinander abgestimmt sind. Es ist generell davon abzuraten, eigene Farbkombinationen zu wählen, da diese oft einen unprofessionellen Eindruck erwecken. Die Hexadezimal-Farbkodierung erhält man entweder durch Nachschlagen in einer Suchmaschine oder durch Nachschauen in den Farbpaletten. Dafür müssen die Packages scales und RColorBrewer installiert und geladen werden.
Die Rottöne aus Abbildung 8.16 wurden bspw. aus der Brewer Farbpalette ausgewählt, welche von ggplot2 direkt zur Verfügung gestellt werden. Zum Anzeigen von 9 Farben der roten Farbpalette kombinieren wir die Funktion brewer.pal() mit show_col(). Beachte die Trennung der Funktionsnamen einmal mit Punkt und einmal mit Unterstrich. Neben den Rottönen könnte man so auch die genauen Farben der Dark2 Palette herausfinden.
Abbildung 8.17: Farbpaletten mit Hexadezimalcodes der Rottöne und Dark2.
Eine ansprechende Farbpalette mit Berücksichtigung von Farbblindheit ist durch die Viridis Palette gegeben. Diese Farbpalette erstellt man mit scale_fill_viridis_d(begin = 0.27, end = 0.72, option = "C"). Wie bei den Graustufen zuvor können auch hier die Start- und Entwerte angepasst werden. Das optionale opt Argument wählt hier die dritte von acht möglichen Viridis Paletten aus. Für kontinuierliche Skalen muss stattdessen auf die Funktion scale_fill_viridis_c() zurückgegriffen werden.
8.10.2 Themen und Achsen
Der hellgraue Standardhintergrund und die fehlende Visualisierung der Achsen ist in der Wissenschaft in der Regel nicht erwünscht. Ein gutes minimales Thema ist theme_classic(). Innerhalb der theme_*() Funktionen kann die Textgröße und -art direkt angepasst werden. Relativ zur Basisgröße (base_size) sind andere Elemente wie Überschriften entsprechend größer. Welches die richtige Größe ist, hängt maßgeblich von den Dimensionen der Abbildung und somit der Auflösung ab (siehe Kapitel 8.12). Weitere Themen sind z.B. theme_minimal() oder theme_bw().
a <- p + theme_classic(base_size = 14, base_family = "sans")
b <- p + theme_minimal()
c <- p + theme_bw() 
Abbildung 8.18: Vergleich verschiedener Themen aus ggplot.
Neben den direkt in ggplot enthaltenen Themen, stellt das ggthemes Package noch weitere Themen zur Verfügung. Die Beschriftung der x-Achse und y-Achse wird mithilfe der Funktion labs() (Akronym für labels, engl. für Beschriftung) angepasst.
Zum Verändern der Textgröße, Textausrichtung und zur Adjustierung, verwenden wir die Funktion theme(). Jedem Argument innerhalb von theme() müssen die Werte (wie z.B. die Textgröße) innerhalb der Helferfunktion element_text() übergeben werden. Das Argument vjust schafft etwas Raum zwischen der Achsenbeschriftung und dem Text der Achsen. Zusätzlichen Platz um die Abbildung herum erhalten wir mit plot.margin. Innerhalb der Funktion margin() können wir so die Abstände nach oben (t), rechts (r), unten (b) und links (l) anpassen. Vor allem oberhalb und rechts der Abbildung ist häufig zu wenig Platz, sodass je nach Dimension Teile der Abbildung abgeschnitten würden.
p +
theme(
axis.title.y = element_text(vjust = 2),
axis.title.x = element_text(vjust = 0.5),
axis.text = element_text(size = 13),
plot.margin = margin(t = 10, r = 20, b = 1 , l = 1, unit = "pt")
)Mit der Funktion scale_x_discrete() verändert man die Reihenfolge diskreter Merkmale auf der x-Achse. So könnte mithilfe des limits Arguments bspw. zuerst der Boxplot für Neurotizismus angezeigt werden. Mit dem labels Argument gibt es die Möglichkeit, die Namen der Merkmale zu ändern. Dabei befindet sich auf der rechten Seite des Gleichheitszeichens der neue Name (hier Extra und Neuro) und auf der linken Seite die alte Bezeichnung. Äquivalent dazu existiert die Funktion scale_y_discrete().
p +
scale_x_discrete(
limits = c("Neurotizismus", "Extraversion"),
labels = c("Extraversion" = "Extra", "Neurotizismus" = "Neuro")
) Für kontinuierliche Skalen gibt es die Funktionen scale_x_continuous() und scale_y_continuous(). Durch das expand Argument wird der zusätzliche Raum zwischen y-Achse und x-Achse entfernt. Außerdem können hier der Anfang und das Ende der Achse (limits) sowie die Anzahl der Beschriftungen eingestellt werden (breaks).
Eine nützliche Funktion für das breaks Argument stellt seq() dar, welche die Abstände der Unterteilungen mit by festlegt.
[1] 0 2 4 6 8 10Ein häufiges Problem sind zu lange Achsenbeschriftung, die sich überschneiden. Um das Problem zu lösen, gibt es drei Möglichkeiten. Man kann die Beschriftungen mit angle (engl. für Winkel) in Kombination mit hjust (Akronym für horizontal adjustment) in einer 45 Grad Winkel bringen.
Eine weitere Möglichkeit ist potentielle Überlappungen innerhalb der Funktion guide_axis() zu überprüfen (check.overlap = TRUE) und die Anzahl der verwendeten Zeilen festzulegen (n.dodge = 2). Dies wurde in mehreren Abbildungen dieses Buches verwendet (z.B. in Abbildung 8.18).
Als dritte Option können lange Beschriftungen mit str_wrap(), einer Funktion aus dem stringr Package, in mehrere Zeilen gebrochen werden (siehe Kapitel 6.9). Wenn bspw. mehr als zehn Buchstaben (width = 10) vorhanden sind, werden die Beschriftungen in mehrere Zeilen gebrochen. Diese Option ist vor allem für Beschriftungen mit mehr als einem Wort nützlich.
Falls die x- und y-Achse mit den maximal möglichen Werten (festgelegt durch limits) enden soll, können wir die Achsen an dieser Stelle mit einer selbsterklärenden Kombination aus der Funktion guides() und guides_axis() abschneiden.
Abschließend fokussiert man mit coord_cartesian() einen Ausschnitt der Abbildung. Dies ist bspw. zur explorativen Betrachtung ohne Ausreißer sinnvoll. Im Gegensatz zu scale_y_continuous() wird in diesem Fall kein Wert gelöscht. Es wird lediglich der neu definierte Ausschnitt vergrößert.
8.10.3 Legende und Facetten
Der Titel und Text der Legende wird am besten über die Farbfunktionen verändert. Beim vorherigen Anpassen der Füllfarbe in Abhängigkeit des Geschlechts, können dabei noch das name Argument für den Titel und das labels Argument für die Merkmalsbezeichnungen hinzugefügt werden.
p +
scale_fill_viridis_d(
begin = 0.27, end = 0.72, option = "C",
name = "Geschlecht (Auswahl):",
labels = c("Weiblich", "Männlich")
)Die Reihenfolge der gruppierenden Variable, die in der Legende angezeigt wird, verändern wir mithilfe von lims() (siehe Abbildung 8.19 (b) im Vergleich zur Ausgangslage (a)).
Zum Ändern der Reihenfolge der Füllfarben für die jeweiligen Merkmale müssen die Faktorstufen vor Erstellung der Abbildung verändert werden (siehe Kapitel 6.10). Alternativ könnten wir an dieser Stelle auch fct_rev() zum Umkehren der Reihenfolge der Kategorien verwenden.
Beim anschließenden Visualisieren verändert sich hingegen nichts im Vergleich zur vorherigen Reihenfolge. Das Ergebnis ist in Abbildung 8.19 (c) illustriert.
ggplot(big5_long, aes(x = Faktor, y = Auspraegung, fill = Geschlecht)) +
geom_boxplot(outlier.shape = NA, position = position_dodge(0.95), alpha = 0.8)
Abbildung 8.19: Verschiedene Reihenfolgen der gruppierenden Variable.
Die Textgröße von Legendentitel und -text werden in der bereits eingeführten theme() Funktion angepasst (siehe Kapitel 8.10.2). Ausgeblendet wird der Titel der Legende mit legend.title = element_blank().
Häufig ist die Positionierung der Legende innerhalb der Abbildung möglich und sinnvoll. Zunächst muss hierfür das Argument legend.positionauf "inside" gesetzt werden. Die eigentliche Position wird über x- und y- Koordinaten über das Argument legend.position.inside festgelegt. Welche Werte hierfür am passendsten sind, hängt direkt von der gewählten Dimension und somit der Auflösung der Abbildung beim Speichern ab (siehe Kapitel 8.12). Meistens Bedarf es dabei einige Versuche mit wiederholtem Speichern mit verschiedenen Dimensionen und Positionen der Legende.
p +
theme(
legend.title = element_text(size = 14),
legend.text = element_text(size = 13),
legend.position = "inside",
legend.position.inside = c(0.25, 0.9)
)Eine horizontale Legende wird mit legend.direction = "horizontal" erstellt. Falls die Legende außerhalb der Abbildung über- oder unterhalb dargestellt werden soll, übergibt man dem Argument legend.position entsprechend "top" respektive "bottom" und streicht das zusätzliche legend.position.inside ersatzlos.
Das Anpassen der Facetten erfolgt innerhalb von theme() mit den strip Argumenten. Dabei kann etwa die Textgröße der Überschrift verändert oder der Hintergrund ausgeblendet werden.
8.11 Anordnen mehrerer Graphen
Innerhalb dieses Buches gibt es diverse Graphen, die nebeneinander in einer Abbildung dargestellt wurden. Dafür muss das patchwork Package installiert und geladen sein.
Der erste Schritt ist das Abspeichern der jeweiligen Abbildungen. Exemplarisch nutzen wir an dieser Stelle das Histogramm, das Streudiagramm, den Boxplot und den Q-Q Plot aus den vorherigen Kapiteln und speichern diese jeweils als a, b, c und d.
a <- ggplot(big5_mod, aes(x = Extraversion)) +
geom_histogram(color = "black", fill = "white", binwidth = 0.2)
b <- ggplot(big5_mod, aes(x = Extraversion, y = Alter)) +
geom_point(position = "jitter")
c <- ggplot(big5_long, aes(x = Faktor, y = Auspraegung)) +
geom_boxplot()
d <- ggplot(big5_mod, aes(sample = Alter)) +
geom_qq() +
geom_qq_line()Anschließend addieren wir die vier Graphen in gewünschter Reihenfolge. Die Funktion plot_layout() spezifiziert unter anderem die Anzahl der Spalten (ncol) und plot_annotation() ergänzt mit dem tag_levels Argument Beschriftungen zu jeder Abbildung (siehe Abbildung 8.20).
Abbildung 8.20: Anordnung mehrerer Graphen
Neben "A" kann der Funktion plot_annotation() außerdem "i", "I", "a" und "1" übergeben werden. Die tag_levels können durch tag_prefix und tag_suffix weiter an die eigenen Bedürfnisse angepasst werden. Außerdem können Abbildungen auch in unterschiedlicher Anzahl neben- und untereinander gesetzt werden. Dafür muss man lediglich die oben stehenden Abbildungen mit vertikalen Linien unterteilen und diese dann durch die Abbildung, die unten stehen soll, teilen (siehe Abbildung 8.21).
Abbildung 8.21: Alternative Anordnung und Benennung mehrerer Graphen.
Falls alle addierten Graphen dieselbe Legende hätten, könnte diese mit guide_area() und dem guides Argument gesammelt angezeigt werden. Dabei wird mit guide_area() die Position der gemeinsamen Legende festgelegt.
Eine weitere nützliche Funktion ist plot_spacer() zum Freilassen eines Areals in der kombinierten Abbildung. Wenn man kombinierte Abbildungen (hier als plots gespeichert) im Nachhinein verändern möchte, müssen diese einzeln angesprochen werden. Da diese als Liste gespeichert sind, erreichen wir dies mit einer doppelten eckigen Klammern (siehe Kapitel 11.4). Mit plots[[1]] extrahiert man so Abbildung a.
Falls dieselbe Änderung alle kombinierten Graphen betrifft, können wir diese mithilfe des &-Operators (anstelle von +) umsetzen.
8.12 Speichern von Abbildungen
Alle Abbildungen der vorherigen Unterkapitel können auf dieselbe Art und Weise gespeichert werden. Die Funktion ggsave() benötigt dafür nur die Argument filename für den vollständigen Dateinamen mit Endung und plot für den Namen der Abbildung, die gespeichert werden soll. Abbildungen können bspw. als .jpg oder .png gespeichert werden.
Wir sollten mit den Argumenten width und height zusätzlich die genauen Dimensionen in der Einheit Zoll festlegen. Hiermit bestimmen wir das Verhältnis von Breite und Höhe sowie die Auflösung. An dieser Stelle möchten wir die Boxplots aus Abbildung 8.15 in einer Datei abspeichern, welche in der Variable p gespeichert sind (siehe Kapitel 8.10). Wir speichern die Abbildung als PNG Dateien namens plotA (Abbildung 8.22 links) und plotB (rechts). Dabei sollen beide Abbildungen dasselbe Verhältnis zwischen Breite und Höhe haben. Allerdings hat die Datei plotB eine doppelt so hohe Auflösung.
ggsave(filename = "plotA.png", plot = p, width = 4, height = 5)
ggsave(filename = "plotB.png", plot = p, width = 8, height = 10)
Abbildung 8.22: Auflösungsunterschiede je nach Größe der gespeicherten Abbildung.
Während die Schriftgrößen und Boxplots links angemessen groß erscheint, ist auf der rechten Seite alles etwas klein. Welches Verhältnis und welche Auflösung in deinem Anwendungsfall die Richtige ist, kannst du nur durch ausprobieren herausfinden.
Zum Abspeichern in anderen Formaten verändert man lediglich die Endung des Dateinamens, die restlichen Argument bleiben gleich (z.B. filename = "plotA.jpeg", filename = "plotA.pdf" oder filename = "plotA.tiff").
Die Größe der Abbildung wird durch die Breite (width) und Höhe (height) festgelegt. Unterschiedliche Größen beeinflussen ebenfalls die Auflösung der Abbildung, sodass man häufig im Nachhinein die Textgrößen der Achsenbeschriftungen anpassen und erneut abspeichern muss. Die gespeicherte Abbildung hat nicht dasselbe Format wie die angezeigte Ausgabe innerhalb von RStudio.
8.13 Exemplarische Erweiterungen
Wir erinnern uns, dass die beiden Gs in ggplot für grammar of graphics stehen. Daraus resultiert nicht nur eine konsistente Anwendung, wie wir es in den bisherigen Kapiteln kennengelernt haben. Zusätzlich gibt es diverse darauf aufbauende Erweiterungen. Durch die gleiche Basis können wir auch die Graphen der Erweiterungen, wie zuvor gelernt, anpassen.
Die meisten Erweiterungen halten sich an eine einheitliche Namensgebung. Vor dem Zweck des Packages steht also auch bei den Erweiterungspackages meistens ein gg (z.B. ggsurvfit, ggfortify oder ggridges). Allerdings halten sich nicht alle an eine konsistente Namensgebung.
8.13.1 Kaplan-Meier-Kurve
Für dieses Kapitel müssen die Packages survival, ggsurvfit und ggsci installiert und geladen werden. Letzteres ist dabei optional für Farbpaletten internationaler Journals.
Wir möchten das Überleben der PatientInnen mit einer Krebserkrankung zuerst insgesamt und anschließend unterteilt nach Behandlungsart graphisch darstellen. Im chemo Datensatz aus dem remp Package interessieren uns dabei vor allem die Spalten Beob_zeit, Status und Behandlung. Die Variable Beob_zeit gibt die Untersuchungszeit in Tagen an und Status beinhaltet die Information über den Tod. Die Variable Behandlung umfasst drei verschiedene Therapiearten in Form der Radiochemotherapie, Chemotherapie und Radiotherapie.
# A tibble: 450 × 3
Beob_zeit Status Behandlung
<dbl> <dbl> <fct>
1 0.833 1 Radio
2 4.80 1 Radiochemo
3 1.46 1 Radio
4 0.922 1 Radio
# ℹ 446 more rowsGesamte Überlebenszeit. Bevor wir eine Kaplan-Meier-Kurve zur Visualisierung der Überlebenszeiten erstellen können, müssen wir zunächst mithilfe der Funktion survfit2() aus dem ggsurvfit Package die Überlebenswahrscheinlichkeiten schätzen. Die Formelschreibweise mit der Tilde (~) nehmen wir an dieser Stelle lediglich zur Kenntnis und gedulden uns für weitere Erklärungen bis Kapitel 9 und 9.5.6.
Mit der Funktion ggsurvfit() aus demselben Package können wir anschließend die Überlebenswahrscheinlichkeiten für den gesamten Beobachtungszeitraum über alle Gruppen hinweg abbilden. Zusätzlich bilden wir das Konfidenzintervall der Kaplan-Meier-Kurve ab und fügen eine Risikotabelle hinzu.
res1 <- survfit2(Surv(time = Beob_zeit, event = Status) ~ 1, data = chemo)
ggsurvfit(res1) +
add_confidence_interval() +
add_risktable()
Abbildung 8.23: Kaplan-Meier-Kurve zum insgesamten Überleben.
Überlebenszeit nach gruppierender Variable. Bei Gruppierung der Überlebenszeiten (auch Strata genannt) ergänzen wir das Modell um die unabhängige Variable Behandlung.
Zum Erstellen der eigentlichen Kaplan-Meier-Kurven verwenden wir erneut die Funktion ggsurvfit(). Das Ergebnis ist in Abbildung 8.24 illustriert. Die Dicke der Linie wird mit dem Argument linewidth festgelegt. Auch für die Risikotabelle gibt es Modifizierungsmöglichkeiten. So könnten wir mit dem Argument risktable_stats anders als in unserem Beispiel neben der Anzahl gefährdeter Personen zum jeweiligen Zeitraum ebenfalls die Anzahl der Ereignisse darstellen (z.B. mit risktable_stats = c("n.risk", "cum.event"))). In Bezug auf die Darstellung der Tabelle kann lediglich die Größe der Überschrift und der Gruppenbezeichnung angepasst werden (z.B. axis.text.y.size = 12 und plot.title.size = 14).
Darüber hinaus möchten wir die zensierten Personen kennzeichnen und das Ergebnis der Überprüfung der Gleichheit der Kaplan-Meier Kurven einblenden (siehe Log Rank Test in Kapitel 9.5.6).
Alle weiteren Anpassungen haben wir weitgehend bereits in Kapitel 8.10 kennengelernt. Die Funktion scale_color_nejm() aus dem ggsci Package visualisiert die Farbpalette des New England Journal of Medicine, lab() passt die Achsenbeschriftungen an, guides() schneidet die Enden der x- und y-Achse ab und theme_classic() vergrößert die Schrift und verändert die Schriftart.
Hervorzuheben ist auf der einen Seite die neue Funktion scale_ggsurvfit(), die sinnvolle Standardwerte für eine Kaplan-Meier Kurve bietet. Um diese wiederrum leicht zu modifizieren, müssen wir dem y_scales oder x_scales Argument eine sogenannte Liste übergeben (siehe Kapitel 11.4). Die Inhalte dieser Liste sind hingegen aus Kapitel 8.10.2 bereits bekannt. Besonders wichtig ist in diesem Kontext das expand Argument. Bei vielen Unterteilungen der x-Achse sowie bei vierstelligen Zahlen überschneidet sich die erste Spalte der Risikotabelle häufig mit den Bezeichungen der Gruppen der Tabelle. Um dem entgegen zu wirken, vergrößern den Abstand zur y-Achse durch Erhöhung des ersten Wertes in expand.
Auf der anderen Seite sind hier die Argumente axis.title.y und axis.title.x erwähnenswert. Mit dem Argument vjust adjustieren wir die Position der Achsenbeschriftungen. Dies ist vor allem für die y-Achse essentiell, da die Beschriftung ansonsten bei langen Gruppennamen (z.B. Radiochemotherapie) weit nach links verschoben wird. Anstelle von Beschreibungen der Gruppen in Form von Text könnte man auch nur die Farben der Gruppierung mit add_risktable_strata_symbol() für Rechtecke oder add_risktable_strata_symbol(symbol = "\U25CF", size = 15) für Kreise anzeigen lassen.
Die einfachste Möglichkeit zum Verändern der Gruppenbezeichnungen als solche (z.B. Chemotherapie anstelle von Chemo) ist die Formatierung der Variable als Faktor mit Überschreibung der labels in der richtigen Reihenfolge (siehe Kapitel 4.3.2 und 6.10). Falls man sich für die Option mit Rechtecken oder Kreisen als Beschriftung der Risikotabelle entscheidet, könnte man die Bezeichnung alternativ auch mit dem labels Argument innerhalb von scale_color_nejm() anpassen.
ggsurvfit(res2, linewidth = 0.9) +
add_risktable(
risktable_stats = "n.risk",
theme = theme_risktable_default(plot.title.size = 14)
) +
add_censor_mark(size = 1.1) +
add_pvalue(location = "annotation") +
scale_color_nejm() +
scale_ggsurvfit(
y_scales = list(expand = c(0, 0)),
x_scales = list(
breaks = seq(0, 15, 1),
limits = c(0, 15.5),
expand = c(0.015, 0))
) +
labs(x = "Years after diagnosis", y = "Survival probability") +
guides(x = guide_axis(cap = "upper"), y = guide_axis(cap = "upper")) +
theme_classic(base_size = 14, base_family = "sans") +
theme(
legend.position = "top",
axis.title.y = element_text(vjust = 3),
axis.title.x = element_text(vjust = -1)
) 
Abbildung 8.24: Kaplan-Meier-Kurven mit Tabelle unterteilt nach Behandlungsart.
Die Abbildung speichern wir abschließend wie gewohnt mit der Funktion ggsave() (siehe Kapitel 8.12).
Möchte man an Stelle der Überlebenswahrscheinlichkeiten lieber kumulative Inzidenzen visualisieren, empfiehlt sich das tidycmprsk Package in Kombination mit dem zuvor kennengelernten ggsurvfit Package. Die Unterschied besteht lediglich darin, dass wir hierfür cuminc() in Kombination mit ggcuminc() verwenden müssen. Auf diese Art und Weise können sogar Szenarien mit zwei möglichen Endpunkten berücksichtigt werden.
Wäre beispielsweise nicht nur der Tod als Endpunkt interessant sondern ebenfalls lebensbedrohliche Blutvergiftungen, könnten wir dies mit dem Argument outcome definieren. Dabei ist wichtig, dass die Variable Status die Informationen über Kein Event, Sepsis und Tod beinhaltet als Faktor mit Kein Event als Baseline kodiert ist (siehe Kapitel 4.3.2 und 6.10).
library(tidycmprsk)
library(ggsurvfit)
res1 <- cuminc(Surv(Beob_zeit, Status) ~ 1, data = df)
ggcuminc(res1, outcome = c("Sepsis", "Tod"))Eine weitere beliebte Alternative zur Erstellung von Kaplan-Meier Kurven ist das survminer Package, welches allerdings beim Anpassen des Aussehens für eine Publikation relativ schnell an die Grenzen kommt.
8.13.2 Residuen überprüfen
Für das schnelle graphische Überprüfen der notwendigen Voraussetzungen in Bezug auf die Residuen, müssen wir erst das ggfortify Package installieren und laden.
Zunächst greifen wir an dieser Stelle etwas vor und erstellen ein lineares Regressionsmodell, welches die Variation in der mittleren Extraversionsausprägung durch Geschlecht und Alter erklären soll (siehe Kapitel 9.5.1).
Dieses Modell kann im Anschluss der Funktion autoplot() übergeben werden. Dies funktioniert auf dieselbe Art und Weise wie für die meisten Regressionsmodelle. Als weiteres Argument kann mit which ausgewählt werden, welche Abbildungen ausgegeben werden (hier 1 bis 4). Das Argument label.repel sorgt dafür, dass der Text, der die Ausreißer beschriftet, die Linien nicht überschneidet. Als letztes wird mit smooth.colour noch die Farbe der Regressionsgeraden auf schwarz gesetzt.
Falls wir die Abbildungen als PNG oder PDF exportieren möchten, müssen wir die vier Abbildungen mit einer doppelten eckigen Klammer zunächst auswählen, um diese in weiterer Folge mithilfe des patchwork Packages zusammenzufügen (siehe Kapitel 8.11). Da die Plots mit ggplot erstellt wurden, können wir das Aussehen wie gewohnt anpassen (siehe Kapitel 8.10).
Abbildung 8.25: Graphische Überprüfung der Residuen.
8.13.3 Ridgeline Plot
Für dieses Kapitel muss das ggridges Package installiert und geladen sein.
Sogenannte Ridgeline Plots erlauben unter anderem den Vergleich von mehreren Dichtefunktionen innerhalb einer Abbildung. In Kapitel 8.2 haben wir die Wahrscheinlichkeitsdichte und somit die Verteilung der Werte für eine Variable angezeigt.
Um mehrere Dichten untereinander innerhalb einer Abbildung zu vergleichen, müssen wir den Datensatz zuerst in das lange Datenformat bringen (siehe Kapitel 6.6).
big5_mod2_long <- big5_mod2 |>
pivot_longer(
cols = Extraversion:Gewissenhaftigkeit,
values_to = "Auspraegung",
names_to = "Faktor"
) |>
relocate(Faktor, Auspraegung)
big5_mod2_long# A tibble: 800 × 14
Faktor Auspraegung Alter Geschlecht O1 O2 O3 O4 O5 O6 O7 O8 O9
<chr> <dbl> <dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Extravers… 3 36 m 5 1 5 1 4 1 5 5 4
2 Neurotizi… 1.9 36 m 5 1 5 1 4 1 5 5 4
3 Vertraegl… 3.4 36 m 5 1 5 1 4 1 5 5 4
4 Gewissenh… 3.3 36 m 5 1 5 1 4 1 5 5 4
# ℹ 796 more rows
# ℹ 1 more variable: O10 <dbl>Durch die Funktion geom_density_ridges() werden die Verteilungen von Extraversion, Neurotizismus, Verträglichkeit und Gewissenhaftigkeit gegeneinander aufgetragen. Zusätzlich übergeben wir das Argument alpha, welches die Deckkraft auf 70% reduziert.
Etwas ungewohnt ist an dieser Stelle, dass wir hier auf der y-Achse die zu vergleichende diskrete Variable abbilden und auf der x-Achse die mittlere Ausprägung des jeweiligen Persönlichkeitsfaktors. Abschließend passen wir noch einige Kleinigkeiten für ein ansprechenderes Aussehen an.
ggplot(big5_mod2_long, aes(x = Auspraegung, y = Faktor, height = after_stat(density))) +
geom_density_ridges(stat = "density", alpha = 0.7, fill = "steelblue") +
labs(x = "Mittlere Ausprägung", y = "") +
scale_x_continuous(expand = c(0, 0)) +
scale_y_discrete(expand = c(0, 0)) +
theme_classic(base_size = 14, base_family = "sans") +
theme(
axis.text.y = element_text(hjust = 0, color = "black", size = 12),
axis.title.x = element_text(hjust = 1, vjust = 0.2, size = 13)
) 
Abbildung 8.26: Ridgeline plots mit angepasstem Thema.
8.14 Anwendungsbeispiel
Wir werden uns abschließend in diesem Kapitel anhand eines Eye-Tracking Datensatzes namens eye_tracking anschauen, wie wir mithilfe der bisher gelernten Funktionen, eine komplexere und optische ansprechende Abbildung kreieren können. In diesem Datensatz wurden zwei Studien miteinander verglichen, die mithilfe von Eye-Tracking die Anzahl der angeschauten Gesichter in Abhängigkeit der gezeigten Informationsdichte gezählt haben.
# A tibble: 100 × 3
Gesichter Dichte Studie
<dbl> <dbl> <chr>
1 142 3.35 Study 1
2 91 3.44 Study 2
3 140 2.81 Study 2
4 56 2.20 Study 2
# ℹ 96 more rowsDie Ergebnisse der beiden Studien sollen anhand eines gruppierten Streudiagramms mit Regressionsgeraden verglichen werden (siehe Kapitel 8.3). Zusätzlich werden gruppierte Wahrscheinlichkeitsdichten zur Darstellung der Verteilungen abgebildet (siehe Kapitel 8.2). Das gewünschte Resultat ist in Abbildung 8.27 illustriert.
Abbildung 8.27: Anzahl fixierter Gesichter in Abhängigkeit der Informationsdichte.
Diese Abbildung besteht im Prinzip aus vier Teilen, welche nacheinander erstellt und dann miteinander kombiniert werden müssen. Links unten ist unsere Hauptabbildung, mit bereits bekannten Komponenten. Um den notwendigen Code besser zu verstehen, gehen wir erst durch, was wir zur Visualisierung benötigen.
- Erstelle den
ggplotmit der Informationsdichte auf der x-Achse und den fixierten Gesichtern auf der y-Achse, wobei die Farbe gruppiert nach der jeweiligen Studie gewählt werden soll. - Füge ein nach Studienart gruppiertes Streudiagramm mit angepasster Größer der Punkte und reduzierter Deckkraft hinzu.
- Zeichne einen schwarzen Ring um jeden Punkt des Streudiagramms.
- Berechne die linearen Regressionsgeraden, welche sich über die komplette Abbildung erstrecken sollen und blende dabei die Konfidenzintervalle aus.
Anschließend soll die Abbildung noch verschönert werden.
- Ändere die x-Achsen und y-Achsen Beschriftung.
- Verwende anstelle der Standardfarben eine Farbpalette (z.B.
viridis), welche auch von Menschen mit Farbenblindheit unterschieden werden kann. Im Zuge dessen sollen der Titel der Legende sowie die Namen der Merkmale angepasst werden. - Passe die Begrenzungen der x-Achse und y-Achse an.
- Verändere das generelle Thema sowie die Schriftgrößen.
- Verschiebe die Legende und ordne sie horizontal an.
Die Hauptabbildung wird schließlich als plot1 gespeichert.
plot1 <- ggplot(eye_tracking, aes(x = Dichte, y = Gesichter, color = Studie)) +
geom_point(size = 3, alpha = 0.8) +
geom_point(shape = 1, color = "black", size = 3) +
stat_smooth(method = "lm", fullrange = TRUE, se = FALSE) +
labs(
x = "Informationsdichte",
y = "Anzahl fixierter Gesichter",
) +
scale_color_viridis_d(
begin = 0.2, end = 0.7, option = "D",
name = "Studie:",
labels = c("1", "2")
) +
scale_y_continuous(
limits = c(0, 225),
expand = c(0, 0),
breaks = seq(from = 0, to = 225, by = 25)
) +
scale_x_continuous(
limits = c(0.5, 4),
expand = c(0, 0),
breaks = seq(from = 0.5, to = 4, by = 0.5)
) +
theme_classic(base_size = 14) +
theme(
legend.position = "inside",
legend.position.inside = c(0.25, 0.95),
legend.direction = "horizontal"
) Bei den beiden Wahrscheinlichkeitsdichten wird erst die Informationsdichte auf der x-Achse in der einen und die Anzahl fixierter Gesichter auf der y-Achse in der anderen Abbildung übergeben. Beide Abbildungen sollen eine etwas niedriger Deckkraft als die Hauptabbildung haben, da sich beide Verteilungen überschneiden werden. Abschließend müssen wir das Thema (auch die Achsen) mithilfe von theme_void() vollständig ausblenden. Auch die Legende muss manuell entfernt werden. Gespeichert werden die beiden Ergebnisse als dens1 und dens2.
dens1 <- ggplot(eye_tracking, aes(x = Dichte, fill = Studie)) +
geom_density(alpha = 0.6) +
theme_void() +
theme(legend.position = "none")
dens2 <- ggplot(eye_tracking, aes(y = Gesichter, fill = Studie)) +
geom_density(alpha = 0.6) +
theme_void() +
theme(legend.position = "none") Als letzten Schritt fügen wir die einzelnen Teile zusammen (siehe Kapitel 8.11). Die Funktion plot_spacer() füllt dabei den leeren Raum oben rechts in der Abbildung aus. Innerhalb von plot_layout() verwenden wir die Argumente widths und heights, welche die Verhältnisse zwischen der Hauptabbildung und den Dichten festlegen. Schließlich soll die Wahrscheinlichkeitsdichte oben links und unten rechts kleiner dargestellt werden als unsere Hauptabbildung unten links. Abschließend muss noch die Füllfarbe für dens1 und dens2 angepasst werden. Beachte an dieser Stelle das Hinzufügen der Funktion mithilfe von & anstelle von +.